ゼロからのレオロジー
増渕 雄一
京都大学化学研究所
レオロジーはそれ自体がコスメ、食品、塗料などの製品の機能として重要なだけでなく、プロセス設計のパラメーターや品質管理の指標としても使われます。しかし書店で入手できる入門書は少ないため、馴染みづらいように思われてはいないでしょうか。本稿では、初学者の方にレオロジーの“さわり”をご紹介し、本格的な教科書に取り組んでいただく手がかりをお示しすることを目的としてお話しします。
レオロジーとは何か
レオロジーとは物質の変形や流動に対する力学的な応答を扱う学問です。モノを流したり、変形させたりしたとき、どんな力で抵抗するかを考えます。似た学問に流体力学と材料力学があります。これらとの違いは、対象とするモノの複雑さです。流体力学や材料力学では、モノの流し方や変形のさせ方が複雑です(例えば自動車のまわりの空気の流れや地震波による原子炉の揺れ)が、モノの振る舞い自体は、ほとんどの場合で単純であることを仮定します。一方、レオロジーでは、流し方や変形のさせ方は単純な場合を扱い、その代わりモノの応答の複雑さを議論します。
レオロジーの研究には主に以下の3つの立場があり、どの立場からアプローチしようとしているかをはっきりさせておくと迷子にならずにすみます。
まず一つ目は、モノを評価する指標としてレオロジーを用いる立場です。モノの変形や流動の様子を定量化し、モノの特徴を数値で表します。
二つ目の立場は、モノの中で何が起きているかを議論するためにレオロジーを用いる立場です。レオロジーで議論されるモノの振る舞いは、すべてモノを構成する分子によってもたらされるものです。従ってレオロジーから分子の振る舞いをも議論することが(原理的には)可能です。専門誌に掲載されているレオロジーの論文は、ほとんどこの立場であり、高分子やコロイド、液晶などのいわゆるソフトマターの解析が多く見られます。
三つ目の立場は上記の二つを踏まえて、レオロジーを機能として用いるために積極的に制御しようとする立場です。コスメ、食品、インクなど、工学的には幅広く求められる立場と言えましょう。
読者の方は三つ目の立場にご関心が高いとは思いますが、本稿では紙面の都合上、一番目の、モノを評価する指標としてのレオロジーについてのみご説明します。
変形と応答
レオロジーでは物質の変形や流動、それに対する応答を議論しますので、それぞれを数値化して定義する必要があります。まず変形と流動ですが、ひずみ(strain)という量と、その時間微分であるひずみ速度(strain rate)、で定量化します。ひずみ量は変形の様式によって定義が異なりますが、ここでは実験的に用いられることが多いせん断変形について、図1に示します。せん断変形は、トランプの山を机におき、一番上のトランプを横にずらすような変形です。この変形の量を示す、ひずみγは、試料の厚みdと上面の移動距離Lにより、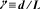 で定義されます。 Lが大きくなる場合だけでなく、試料の厚みdが小さくなる場合でも、ひずみγが大きくなることに注意してください。ひずみは無次元量で、ひずみ速度の次元は(sec-1)となります。ひずみ速度はdγ/dtですが、
で定義されます。 Lが大きくなる場合だけでなく、試料の厚みdが小さくなる場合でも、ひずみγが大きくなることに注意してください。ひずみは無次元量で、ひずみ速度の次元は(sec-1)となります。ひずみ速度はdγ/dtですが、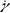 と表されることがよくあります。せん断変形の他に伸長変形もありますが、装置を作成しづらいことなどから、あまり議論されません。(ただし紡糸、フィルム伸長、ブロー成形、急縮小流れ、発泡、などの工程では重要になりますので、適当な参考書を御覧ください。)
と表されることがよくあります。せん断変形の他に伸長変形もありますが、装置を作成しづらいことなどから、あまり議論されません。(ただし紡糸、フィルム伸長、ブロー成形、急縮小流れ、発泡、などの工程では重要になりますので、適当な参考書を御覧ください。)
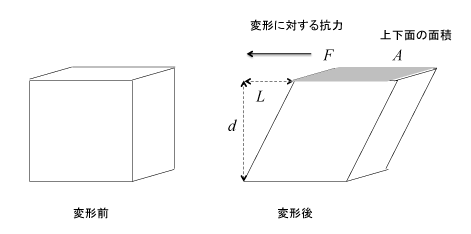
図1 せん断変形
工業的なプロセスにおけるひずみ速度を知っておくことはレオロジーを理解する上で極めて重要です(表1)。私たちの生活において、物質は広範なひずみ速度下にあることがわかります。たとえばインクの場合、保存時に重要な重力下での沈降や、塗布後のレベリングに対して、塗布の過程は数桁も高いひずみ速度を与えることがわかります。物質のレオロジーを評価したり、制御したりする場合は、どのような工程を想定するのか、それぞれの工程でのひずみ速度を想定しておく必要があります。
次に変形に対するモノの応答ですが、応力(stress)という量で表します。応力は圧力と同じ次元( Pa = N m-2)で表されます。せん断変形に対して通常議論されるせん断応力は、変形に対する抗力Fと試料の上下面の面積Aで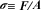 で定義されます(図1)。
で定義されます(図1)。
表1 様々な工程のせん断速度[1]
| 工程 | せん断速度(sec-1) |
|---|---|
| 粒子の沈降 | 10-6 - 10-3 |
| 表面張力によるレベリング | 10-2 - 10-1 |
| 重力による液ダレ | 10-1?10 |
| 押し出し | 1 ? 103 |
| カレンダリング | 10 - 102 |
| ボトルからの流出 | 10 - 102 |
| 噛む、飲む | 10 - 102 |
| ディップ | 10 - 102 |
| 混合、攪拌 | 10 - 103 |
| ラビング | 102 - 104 |
| ブラッシング | 103 - 104 |
| スプレー吐出 | 103 - 105 |
| 潤滑 | 103 - 107 |
物性量
ひずみと応力、または、ひずみ速度と応力の関係から、物性量が定義されます。
まず、固体の硬さを表す量として弾性率(modulus)があります。中学校の理科で習う、バネのフックの法則を思い出してください。バネの伸びと力は比例し、その比例係数はバネ定数と呼ばれました。つまり力をF、伸びをx、バネ定数をkとすると、F = kxの関係がありました。同様の関係が、ひずみγと応力σに成り立つとき、バネ定数に相当する比例係数を弾性率と呼びます。すなわち、σ=Gγと表せるときのGが弾性率です。この式をみてわかるように、(ひずみγには単位がないので)弾性率Gの単位は応力σと同じPaとなります。 Gが大きいモノは、大きな力をかけても少ししか変形できないので、硬い物質ということです。逆にGが小さければ、少しの力で大きく変形できるので、柔らかい材料ということです。
また、液体の流れやすさを表す量として粘度(viscosity)があります。高等学校までで習わないので、あまりなじみがないと思いますが、バネのフックの法則に対応して、液体にはニュートンの法則というものがあります。ニュートンの法則では、応力σはせん断速度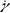 に比例し、
に比例し、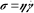 と表せるとします。このときの比例係数ηが粘度(または粘性係数)です。ニュートンの法則を理解するには、お風呂に入ってお湯の中で腕を動かして見てください。腕を速く動かそうとすると強い力が必要です。ゆっくり動かせばそれほど力は必要なく、全く動かさなければ力は不要です。これがニュートンの法則で、腕を動かすのに必要な力は、腕を動かす速さに比例することがわかります。ηが大きいモノは、大きな力をかけても早く流せませんので、粘い液体です。ηの単位は(σの単位がPa、
と表せるとします。このときの比例係数ηが粘度(または粘性係数)です。ニュートンの法則を理解するには、お風呂に入ってお湯の中で腕を動かして見てください。腕を速く動かそうとすると強い力が必要です。ゆっくり動かせばそれほど力は必要なく、全く動かさなければ力は不要です。これがニュートンの法則で、腕を動かすのに必要な力は、腕を動かす速さに比例することがわかります。ηが大きいモノは、大きな力をかけても早く流せませんので、粘い液体です。ηの単位は(σの単位がPa、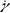 の単位がsec-1であるため)Pa secとなります。
の単位がsec-1であるため)Pa secとなります。
弾性率と粘度に加えてもう一つ知っておきたい量として、降伏応力σy(yield stress)があります。後で述べるように、物質の中には塑性体と呼ばれる一群があります。塑性体は粘土や口紅のように、ある一定以上の力を与えたときだけ流れる性質をもつモノの総称です。この、塑性体を流すために必要な最小の力を降伏応力と呼びます。
様々な物質の弾性率と粘度を表2、3に示します。レオロジーは人間の感覚を数値化する側面があります。身の回りの物質について粘度や弾性率を数値として知っておくと、論文や特許のデータを見るときに良い基準となります。たとえば骨の弾性率は1010Paで、肉(生体組織)の弾性率は105Paです。人間が触覚でモノの硬さを感じるときのことを考えると、1010Paよりも硬いモノは、指の骨の方が変形してしまうため、いくら硬くても同じに感じる(骨の硬さを感じてしまう)ことになります。一方、105Paよりも柔らかいものは、いくら柔らかくても同じに感じる(肉が変形できないので柔らかさが感知できない)ことになります。従って、人間が「ぐにゃぐにゃしている」などと感じることができるのは、105Pa ? 1010Paの間の硬さをもつものだけです。表2を見ると、プラスチックやガム、ゴムなど、確かにそのような物質が該当する弾性率を持っていることがわかります。
表2 様々な物質の弾性率
| 物質 | 弾性(Pa) |
|---|---|
| 炭素繊維/ 鉄/ ガラス | 1011 |
| コンクリート/骨/氷/木 | 1010 |
| ポリエチレン/バター | 108 |
| ゴム/チョコレート | 107 |
| ガム(食前) | 106 |
| ガム(食後)/ゆで卵/生体組織 | 105 |
| マヨネーズ/ケチャップ | 103 |
| ヨーグルト | 102 |
| 生卵 | 10 |
表3 様々な物質の粘度
| 物質 | 粘度(Pa sec) |
|---|---|
| ヘリウム4 | 0 |
| 空気 | 10-5 |
| 水 | 10-3 |
| マヨネーズ | 1 |
| ハチミツ | 10 |
| 溶岩 | 102 - 106 |
| 粉雪 | 104 - 109 |
| 氷 | 1014 |
| マントル | 1022 |
レオロジーによる物質挙動の分類
上記で定義された変形と応答により、物質のレオロジー挙動を分類することができます。図2は英国レオロジー学会によってなされたものです。左端が理想弾性体で、フックの法則(ひずみと応力が比例関係にある)に従うものです。応力を取り除くとひずみは瞬時にゼロに戻ります。つまり変形は即座に回復し、物質は流れません。反対に右端は理想粘性体で、ニュートンの法則(ひずみ速度と応力が比例関係にある)に従うものです。この場合は応力を取り除いても変形は消えずに残ります。つまり物質は流れます。この二つは固体と液体の理想的な状態といえますが、この間に多様な振る舞いが含まれています。
まず左端から3つは固体で、力を取り除いたとき変形がゼロに戻ります。左から2番目は弾性率がひずみに依存して変化するもの(非フック弾性)、3番目はさらに時間にも依存するもの(粘弾性固体)です。
一方右端から3つは液体で、力を取り除いても変形が残ります。右から2番目は粘度がひずみ速度に依存して変化するもの(非ニュートン流体)、3番目はさらに時間にも依存するもの(粘弾性液体)です。
中央に位置する3つは、加えられる力の大きさによって固体と液体を遷移するもので、塑性体と呼ばれます。中央3つのうち右端がビンガム流体と呼ばれる塑性体の理想形で、降伏応力以上の力が加わったときにはニュートン粘性と同様に振る舞います。その左隣は粘度がひずみ速度に依存します。さらに左端のものは力を取り除いた後、変形が回復して固体的に振る舞います。
下部にある図のうち、上段は物体に一定の力を与え続けたときの変形挙動を、縦軸をひずみ、横軸を時間として示している。破線は力を取り除いた後の挙動。下段は応力が横軸、縦軸はひずみ(左から3番目まで)またはひずみ速度(それ以外)。[なお、この図ではひずみがσで、応力がSで書かれており、本文の定義とは異なるので注意。]
興味あるレオロジー挙動1:非ニュートン流体
図2の右から2番目にある非ニュートン流体は工業的に重要です。このカテゴリーに分類される流体では、粘度がせん断速度に対して一定ではありません。ニュートン流体では粘度は一定なので、ニュートン的でない、という意味で非ニュートン流体(Non-Newtonian fluid)と呼ばれます。応力とひずみ速度の関係を示した、図2の下段の図において、それぞれの線の傾き(応力をひずみ速度で割ったもの)が粘度に相当します。得られた粘度とひずみ速度の関係は図3になります。破線で描かれているのはニュートン流体で、粘度が一定です。これに対して粘度がひずみ速度に対して低下するもの(シアシニング)と、増加するもの(シアシックニング)があることがわかります。
シアシニング流体は身の回りにあふれています。たとえばインクは、重力場では(低せん断速度域では)液ダレして欲しくないので粘度が高いですが、塗布時には(高せん断速度域では)粘度は低くなっています。(これには材料内部のミクロな構造が関わっています。)
シアシックニング流体はプロテクターやスポーツ用品に応用されています。プロテニスの世界ランキング上位に位置するジョコビッチ選手が使用するラケットのリムに入っており、ラケットに加わる変形の速さでガットの張力が自動的に変わるようになっています。すなわち、ロブなどのときには柔らかく、スマッシュなどのときには硬くなるのです。アメリカでは防弾チョッキへの応用も考えられています。
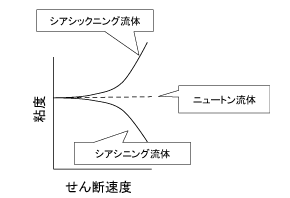
図3 非ニュートン流体
興味あるレオロジー挙動2:塑性体
図2の中央にある塑性体は粘度、口紅、バター、ヨーグルト、あるいは物理ゲルで見られる挙動です。ハミガキも塑性体で、その降伏応力は重力により与えられる力よりも少し大きいくらいになっています。つまり、重力だけでは固体となって動かないため、歯ブラシの上で流れずに留まってくれる一方、降伏応力が小さいため、チューブからは容易に押し出せるのです。チューブ入りの液状の接着剤などと比べると、ハミガキの扱いやすさがよくわかります。このハミガキの塑性体としての性質は決して自然にできたものでなく、ハミガキがチューブ入りとなった20世紀に入ってから人工的に付与されたものです。またエレクトロレオロジー流体と呼ばれる物質では、降伏応力が電場によって変化します。 これを応用してロボットの間接やアクティブダンパーなどが開発されています。
興味あるレオロジー挙動3:粘弾性
図2の右から3番目の粘弾性液体、左から3番目の粘弾性固体は、それぞれ弾性率が時間変化する点に特徴があります。このように弾性率が時間変化する流体を粘弾性体(Viscoelastic body)と呼びます。身の回りにあるモノのなかではチューインガムをイメージしていただくとわかりやすいと思いますが、実際には多数の物質が粘弾性(つまり弾性率の時間変化)を示します。弾性率の時間変化はモノの内部の分子運動を反映するものであるため(冒頭で述べたレオロジーの使い道では2番目にあたる)、レオロジーを用いて材料内部を調べる場合は粘弾性挙動に注目します。
粘弾性を調べる場合は、緩和時間という概念が重要です。これは図2の上段にあるグラフで見ると、外力を取り除いたとき、ひずみが回復するまでの時間(点線がゼロに戻る時間)です。この時間は、モノの内部での分子運動の時間に相当しています。具体的には、分子がブラウン運動によって1回転するくらいの時間です。
粘弾性はレオロジー挙動の一部に過ぎませんが、ソフトマターと呼ばれる物質のダイナミクスを調べるのに適していることから発展しており、レオロジーといえば粘弾性、のようになっている傾向があります。
(2013年1月)
参考文献
[1] J. F. Steffe, Rheological Methods in Food Process Engineering, 2nd Ed., Freeman Press 1997
[2] The British Rheologists Club、 Nature 149 702 1942
お勧め図書
本格的に学びたい方… 尾崎邦宏 「レオロジーの世界」森北出版 (2011)
レオロジーおもしろ話… 増渕雄一 「おもしろレオロジー」技術評論社 (2010)






![レオロジー挙動による物質の分類[2]](/lab/column/27/img/masubuchi_z02.png)